


Introduction to Fourier Analysis |
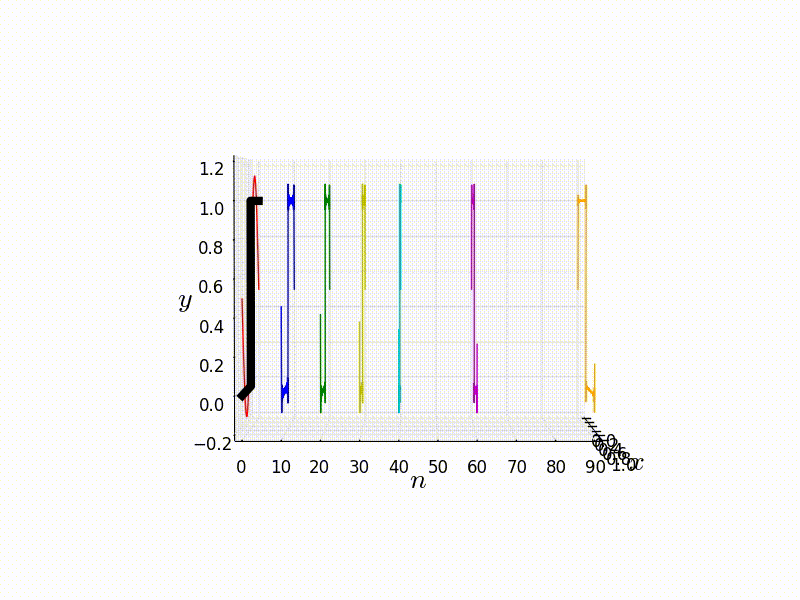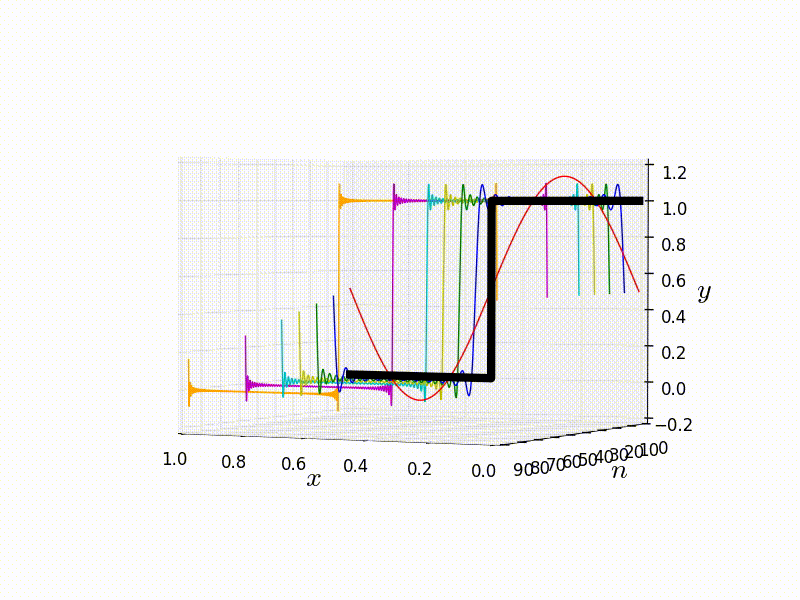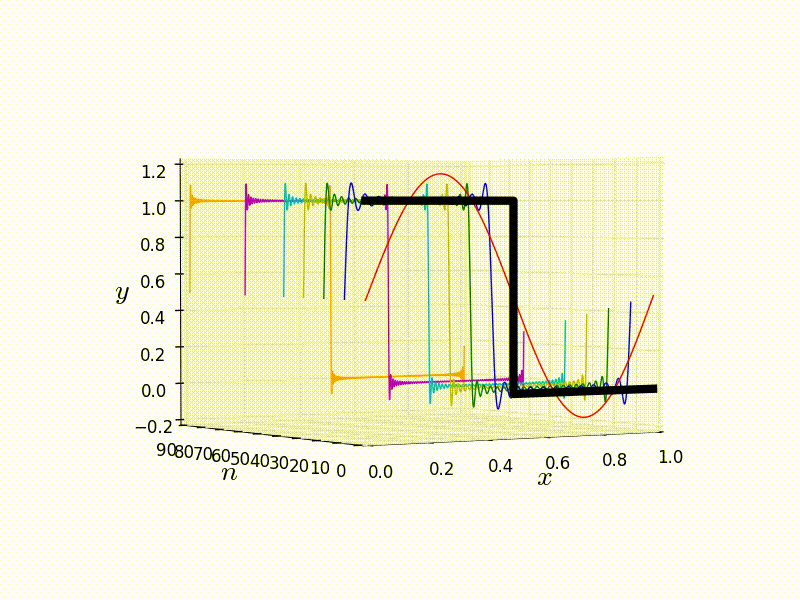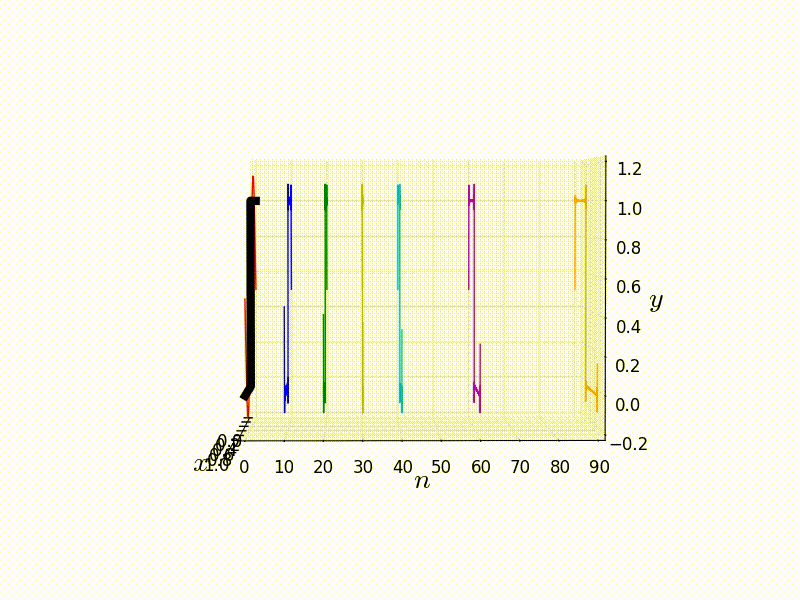
Fourier analysis is a key mathematical tool in a scientists arsenal, and is used across the all fields in then natural sciences as well as other disciplines such as engineering. The first topic is that of the Fourier series, which allows for the representation of a periodic function as a summation of sinusoidal components, which has a wide variety of applications such as signal processing and solving partial differential equations like the heat diffusion equation. The second topic is that of integral transforms, specifically Fourier and Laplace transforms. The former is a natural extension of Fourier series, with an equally wide range of applications. For example; some time varying sound wave can be instead represented as a distribution function in frequency space rather than the usually spatial coordinates.
This is the course page for Introduction to Fourier Analysis (ID: 014003) in the winter semester 2020. Lectures will be held in room 202 in Science Building 5 Lectures will be held via Zoom, details can be found on Moodle, from 8:45 - 10:15 (1st period) Thursday. The material will be the subject of seminars held immediately after each lecture.
If you wish to contact me my email address is: alex@oia.hokudai.ac.jp and I can be found in room 2-9-11 (Science Building 2, 9th floor, room 11).
The table of Laplace transforms that we used for reference can be found here.
The examples from the lectures can be downloaded from here.
The 2019 exam can be found here.
Part 1 [26/11] Introduction, derivation of Fourier series.
Part 2 [3/12 + 10/12] Properties of Fourier series.
Part 3 [17/12] Applications of Fourier series.
Part 4 [07/01] Integral transforms.
Part 5 [14/01] Solving PDEs with Fourier analysis.
Exam [21/01]