宇宙物理学-２０世紀から２１世紀へ
Astrophysics in the 20th and 21th century
羽部朝男（北海道大学理学研究科）
Asao HABE (Hokkaido university)
アブストラクト
２０世紀は、宇宙物理学が大きく進展した時代であった。宇宙に対する認識は大きく広がり、いまや宇宙の年齢や元素の起源、銀河の形成が議論できるようになった。このような２０世紀の宇宙物理学のめざましい成果は、どのように生まれてきたのか。それは物理学の進展と観測技術の発展と深く関係している。この連載では、２０世紀の宇宙物理学の発展を振り返りながら、２０世紀から２１世紀にかけて宇宙物理学が目指している研究を紹介する。
キーワード 宇宙物理学、宇宙論 keywords : astrophysics, cosmoplogy
1. ２０世紀までの宇宙観
宇宙に対する関心は、人類が文明を持つようになってから、たえることなく抱き続けた。
この世の始まりはあるのか
なぜ我々は存在するのか
この世の果てはどうなっているのか
天は落ちてこないのか
多くの文明が生まれる中で、人類はこのような疑問をもっていたのであろう。この最後の疑問は、杞憂（杞人の憂い）の語源となっている。くよくよ考えても起こるはずのないことを「それは杞憂だよ」という。天は落ちてくるはずないじゃないかというわけである。東洋の宇宙に対する関心のうすさをあらわしていて興味深い。そのことと「科学の発展における東洋と西洋との違い」との関連は興味があるところである。
上で述べた疑問の答えを得ようと、人類は古代からさまざまな宇宙像を抱いてきた。宇宙像は、科学の発展とともに、より合理的なもの科学的なものに発展してきた。
地球は動いていない、動いているのは天球である、さらに天球上を月と太陽は運動し、惑星は複雑な運動をしている。このような天体の見かけの運動に対して天動説は一応の定量的な記述に成功した。しかし、ガリレオなどの科学的な探求を否定するドグマに陥った。これに対して、地動説は、惑星の運動や明るさの変化ついての観測結果に基づき惑星の運動に対する合理的な説明を与える。ガリレオそしてニュートンによって力学がつくられた、その成果が惑星運動に適用され、惑星や彗星の運動を見事に説明することができた。ニュートン力学の妥当性は彗星の回帰の予言で立証されたことは、よく知られている。
このように宇宙に対する認識の深化とともに、我々人類の位置が宇宙の中心から、どんどん離れていったことは興味深い。２０世紀の宇宙物理学の発展は、宇宙の広がりの認識を深めていくとともに、人類が宇宙の中心から離れていることを認識する過程でもあった。天動説では、地球は宇宙の中心に位置していた。地動説では、太陽系が宇宙の中心となった。しかし、太陽が宇宙の中心ではない。１９世紀には太陽系を取り巻く恒星の世界（天球）については、無限に広がっているとした場合の問題点（たとえばオルバースのパラドックス）が認識されていた。すでに、ニュートンは宇宙の構造について彼の重力理論を用いて考察している。その結果、無限に広がった宇宙の問題点を認識していたと言われている。しかし、太陽系をこえた宇宙がどうなっているのかを人類が知るのには２０世紀を待たねばならなかった。
２０世紀の科学の進展はめざましく、宇宙物理学もその例外では無い。コペルニクス的転回とも言うべき認識の大転回が２０世紀の宇宙物理学にも起こったのだ。以下で、それをたどっていこう。
2. ２０世紀の宇宙物理学
２０世紀以前は、宇宙とは「太陽系が中心にあり、恒星の世界がそれを取り巻く」という認識であった。２０世紀にはそれが大きく変わって、「銀河を主要な構成要素とする膨張宇宙」という認識に広がっていった。さらに、宇宙が膨張していることから、宇宙の初期は高温高密度な状態であり、宇宙の膨張とともに物質が進化してきたと考えられた。宇宙の元素の起源が議論され、その起源と関連した観測事実として宇宙背景放射が予言され実際に観測された。はじめは、ほぼ一様だった宇宙が、膨張と共に複雑な構造になってきたことが明確になってきたのである。
また、２０世紀は宇宙を観測する手段が飛躍的に広がった時期でもある。従来の光（可視光）の観測に加え、電波、赤外線、Ｘ線で宇宙を観測することが可能になった。その結果、それまで静かな宇宙というイメージが大きく変更を受け、ダイナミックな現象が宇宙で数多く起きていることが明らかになった。地上では再現できないような高温高密度の状態が宇宙で発見された。ブラックホールや中性子星、原始星、クウェーサー、電波銀河やＸ線銀河団などが次々と見つかった。そして、２１世紀を迎える今、宇宙全体の構造を明らかにしようとする研究が進展している。
この連載では、このような２０世紀の宇宙物理学の発展と２１世紀を目指して計画されている観測計画を紹介する。まず、今回は宇宙の膨張が見いだされるまでを述べよう。それは、２０世紀はじめ、アインシュタインの相対論の成立と巨大望遠鏡の建設で始まる。
３ 膨張宇宙の発見前夜、アインシュタインと宇宙モデル
２０世紀はじめに、アインシュタインは特殊相対論を完成させ、それを一般相対論に発展させた。１９１７年に一般相対論を宇宙全体に適用し解を求めた。このとき、アインシュタインは宇宙は一様等方であると仮定した。この仮定の理由は、ニュートンの議論に戻るとわかりやすい。以下それを紹介しよう。
3.1 宇宙は一様等方
宇宙全体が一様等方である可能性は、すでにニュートンによって議論されていた。彼は太陽系が天球に対して運動しているように見えないことから宇宙の物質分布には（つまり恒星の分布には）端はないと考えた。まず、我々が宇宙の中心にいないということを出発点としよう。コペルニクス的転回によって我々が宇宙の中心にいるとは考えられないからである。そうすると、宇宙に端があれば、我々のまわりの物質の分布には方向によって偏りがでることになる。その偏りは重力として表れるはずである。しかし、太陽系がこのような重力を受けているという証拠が無い。重力に偏りがないためには端がなければ良い、というわけである。つまり、宇宙を満たしている物質は密度が一様でどこまでも分布しているはずであり、どの方向にも同じように物質は分布していると考える。このような考えを宇宙原理と呼んでいる。
3.2 アインシュタインの静的宇宙モデル
アインシュタインは、この宇宙原理に基づいて宇宙の構造に関する一般相対論の解を求めようとした。宇宙は一様で等方的であり、かつ、静的であるとした。これは、恒星が天球上でほとんどその位置を変えていないことからも当然と考えられた。しかし、アインシュタインは静的な宇宙の解は見つけられなかった。それは、一般相対論は重力を記述する相対論であり、一様に物資が存在して入れば、重力によって収縮が起こり静的なつりあいのままでいられないからである。彼は、アインシュタインの方程式に宇宙項と呼ばれる項を付け加えて静的な解を得た。（彼は、宇宙項を付け加えたことを後年悔やんだそうだ。しかし、最近ではこの宇宙項の有無が議論されている。）
3.3 フリードマンの膨張宇宙モデル
このようなアインシュタインの研究ののち、ドシッター(1917)やフリードマン(1922)が膨張している宇宙の解を求めた。フリードマンがアインシュタイン方程式から求めた一様等方宇宙を記述する方程式がどのようなものか見てみよう。
この方程式のaは宇宙の大きさを表すスケールファクターと呼ばれるものである。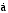
はaの時間微分、つまりスケールファクターの変化する時間的割合、すなわち速度である。ρは宇宙の平均密度、Gは重力定数である。kは宇宙の曲率を表しているパラメーターである。k＝１のときは宇宙は閉じており、k＝０のときは宇宙は平坦であり、k=-1のときは宇宙は開いていると呼んでいる。Λは宇宙項である。以下では、Λ=0としよう。また、宇宙に分布している物質の圧力が無視できる場合、4πρa3/3は保存することがアインシュタイン方程式から導かれる。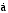とすると、この式は質量M=4πρa3/3による重力のもとで半径方向に運動する単位質量の質点の力学的エネルギーの保存則に対応している。つまり、aは質点の位置、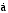は質点の速度、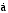の２乗の1/2は運動エネルギーに対応する。よって上式の左辺は、この質点の単位質量あたりの力学的エネルギーに相当する。つまり、この式は、地球上で質点を真上に投げあげた時の質点の運動についての力学的エネルギー保存の式と同じ形をしている（ここの議論では地球の自転のことは考えていない）。このことからaの時間変化は直感的に理解できる。以下では、この質点の運動のアナロジーでaの時間変化について説明しよう。
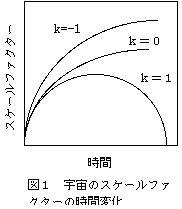
aが時間とともに増大する場合（つまり質点を投げあげた場合）、この質点は重力によって引かれているので、aの増大とともにその速度は減少する。k=1のときは力学的エネルギーが負であるのでaは無限に大きくなることはない。aがある大きさに達すると速度がゼロになり、その後、速度は負になりaは減少する。また、k=0の時はaが増大し続け、aが無限大のところで速度がゼロになる。また、kが負であるとaが無限大になると速度は有限な一定の値に近付く。このようにkの値によって宇宙のスケールファクターの時間変化が異なる。つまり、k=1なら宇宙のスケールファクターは増大したあと減少に転じ、a=0に近づいてゆく。このような変化の様子を模式的に次のグラフ９図１）に示した。
k=0あるいはk=-1なら宇宙のスケールファクターは時間とともに増大しつづける。宇宙のスケールファクターの時間変化と宇宙が閉じているか、開いているか、平坦であるか、が対応している。また、4πρa3/3は保存するので、宇宙のスケールファクターaが変化することによって宇宙の物質密度ρが変化する。つまりaの増大とともにρは減少する（この関係は宇宙を構成している物質のエネルギーが光のエネルギーに比べて大きい場合に適用できる。光のエネルギーのほうが大きい場合にはこの関係とは別の関係が得られる）。
このaの時間変化は何に対応しているのだろうか。それには、宇宙のスケールファクターと宇宙の各点の座標との関係を知る必要がある。フリードマン方程式では、一様な宇宙の中の空間的な位置の座標をa(t)rであらわしている。宇宙の全体的な膨張はa(t)が表している。よって、宇宙を構成している天体が宇宙全体の膨張とともに膨張しているとその天体の速度は(da(t)/dt)rとなる。この場合、天体の速度は(da(t)/dt)r＝{(da(t)/dt)/a(t)}a(t)rのように距離a(t)rに比例することになる。これが、膨張している宇宙の特徴である。このときの比例係数(da(t)/dt)/a(t)が重要な意味を持っている。
宇宙の構造を知るためには、現在の膨張速度とスケールファクターの比(da(t)/dt)/a(t)と宇宙の密度の値ρを知る必要がある。これがわかるとフリードマン方程式を用いてkを求めることができ、宇宙の膨張が将来どのようになるかを推測することができる。このようにフリードマンが求めた宇宙の解は時間とともにそのスケールファクターが増大あるいは減少するものである。現実の宇宙が膨張していることを示す観測的事実が、この解が発見されてから数年して得られた。
４ 巨大望遠鏡の建設と膨張宇宙の発見
１９世紀にハーシェルは、恒星が天球上で一様に分布しているのではなく、天の川に集中して分布しているらしいことを示した。このような恒星の世界がどのような構造を持ち、どこまで広がっているのかを明らかにするには、より遠くの天体の距離の測定が可能になることが必要であった。２０世紀に入り、巨大な望遠鏡が建設されることによって観測が飛躍的に進んだ。セファイド型変光星の周期光度関係（１９１８年）が発見され、遠くの恒星や銀河までの距離の測定が可能になった。その結果、宇宙の構造がしだいに明らかになったのである。
4.1 天体の距離の測定法
a）年周視差
宇宙の構造を探るには天体までの距離を知る必要がある。はじめに、この距離の測定方法について簡単に紹介しよう。天体の距離を測定する最も基本的な方法は、年周視差を利用する方法である。年周視差は、地球が太陽のまわりの公転軌道を半周するあいだに恒星の見える方向が変化することを言う。この年周視差を利用してその恒星までの距離を測定することができる。年周視差をΔθラディアン、地球の公転半径をaとすると、恒星までの距離dとの間に
a=dΔθ
の関係がある。これは基本的に三角測量の原理である。Δθを観測から求めると恒星までの距離は
ｄ＝a/Δθ
の関係から求めることができる。Δθが小さな恒星のほうがΔθの大きな恒星よりも距離が遠いことになる。しばしば、宇宙物理学では距離の単位として、この年周視差が１秒角（3600分の１度）になる距離を1pcと定義して用いている。１pcは3.26光年である。
残念ながら、この方法で距離を測定できるのは太陽に近い恒星に限られる。この理由は、当時の大きな望遠鏡でも地上からの可視光の観測では大気の揺らぎによって影響され１秒角の角度分解能しかなく、これを大きく超えた精度で年周視差を測定することは困難であったからである（このような困難を克服するため望遠鏡を大気圏の外に打ちあげて年周視差の測定を行うヒッパルコス衛星が活躍した）。それでは年周視差を検出できないような遠くの天体までの距離はどのように測定するのであろうか。
b)標準光源
その方法は、光度L（単位時間あたりに放射されるエネルギー量）があらかじめわかっている天体（これを標準光源と呼ぶ）を利用するのである。同じ光度Ｌの天体でも見かけの明るさmは天体までの距離に応じて変化する。この関係は、見掛けの明るさmが
m ∝Ｌ／ｄ2
のように光度Ｌに比例し、距離ｄの２乗に反比例することである。Ｌがわかっている場合、mを測定し、この関係を使って距離dを推定できる。このＬを知ることができる天体としてはＬが大きいものほど都合が良い。それはＬが大きければ、遠くにあっても観測が可能になり、より遠い距離を測定するのに使えるからである。このＬを知ることができる明るい天体のひとつがセファイド型変光星である。セファイド型変光星の光度を知る方法は２０世紀はじめにアメリカの天文学者リヴィットとシャープレイによって明らかにされた。
4.2 セファイド変光星の光度周期関係
リヴィット（１９１２）はマゼラン星雲の写真乾板の中に、セファイド型変光星を多数見つけ、その見かけの明るさと変光の周期に一定の関係があることを見つけた。マゼラン星雲の中のセファイド変光星はほぼ同じ距離にあると考えてよいので、見かけの明るさの違いは光度の違いを表していることになる。このことから見かけの明るさと周期との関係は、光度と周期が関係があることを示している。シャープレイ（１９１８）は、近くのセファイド変光星の年周視差を測定に成功し、その結果を使って光度を求めた。その結果、セファイド変光星の光度ー周期関係を得ることができた。つまり、セファイド変光星の周期を測定すれば光度を知ることができる。その光度と見かけの明るさと比較することでそのセファイド変光星までの距離を測定することができる。シャープレイはこの方法をもちいて球状星団や我々の近くの銀河の距離を測定した（この方法は、最近もハッブル望遠鏡のキープロジェクトでも使われている。つまりこの方法は古くて新しい方法なのである）。実はこの方法は、当初あまり成功しなかった。その理由は、セファイド変光星には２種類あることを知らなかったためである。このことは、その後の観測でわかってきた。この点については後で述べることにしよう。
4.2 我々の銀河の大きさ
さて、２０世紀のはじめに話を戻そう。１８世紀にはハーシェルが星を数えて我々の銀河の構造について先駆的な研究を行った。その後、多くの恒星が天の川にそって分布していることが明らかになった。２０世紀に入ってシャープレイが球状星団の分布を調べ、球状星団がいて座の方向を中心としてほぼ球状に分布していることを示した。シャープレイはセファイドの光度ー周期関係を用いて球状星団までの距離を求めた。その結果球状星団の分布の中心までの距離は約１０ｋｐｃ（３０万光年）であることを示した。これは我々の銀河系の中心と太陽系との間の距離をあらわしている。我々の銀河の大きさは太陽系の大きさ（太陽と冥王星との間の距離は約60億キロメートル）をはるかにこえたものであることがわかったきたのである。そして、多くの恒星はこの中心のまわりに回転して円盤状に分布していることがわかっている。これが、我々の銀河の構造である。
4.4 渦巻き星雲を巡る論争
アンドロメダ星雲（現在ではアンドロメダ銀河と呼ばれるがここでは当時の呼び名を使うことにする）は肉眼で見えるほど比較的明るい。星雲と呼ばれるように薄く広がった円盤を傾けたように見える天体である（渦巻星雲と呼ばれた）。２０世紀はじめに、この星雲は我々の銀河と同じように恒星が円盤状に分布しているものか、それともガスが円盤状に分布しているのか、その正体をめぐって論争があった。この論争に決着をつけたのはハッブルであった。1924年ハッブルはアンドロメダの外縁部を星に分解することに成功した。（下の図は、参考のために、最近のハッブル望遠鏡による銀河NGC1365の外側の星を分解したものを示した。）
これによってアンドロメダはガス星雲ではないことが明確になった。さらに、ハッブルはアンドロメダにセファイド変光星を見いだした。さっそく、セファイド変光星の周期を測定して光度ー周期関係から光度を求め、見かけの明るさと比較してアンドロメダまでの距離を求めた。求めた距離は約１００万光年であった（現在ではこの値は約２００万光年に修正されている）。アンドロメダの大きさは、我々の銀河に相当する大きさの恒星の集団すなわち銀河であることが明確になったのである。
4.5 天体の運動
ここで、少しわき道にそれて、アンドロメダ銀河の運動について触れておこう。アンドロメダ銀河は我々の銀河に向かって毎秒300ｋｍというものすごい速度で近づいている。上で求めたアンドロメダ銀河までの距離をこの速度で割ると２０億年になり、およそ２０億年後にはアンドロメダ銀河と我々の銀河は大衝突をすることになる（このアンドロメダ銀河の接近は宇宙における構造形成と関係している）。このとき、何が起こるかは興味深いところである。さて、このような天体の速度はどのようにして測定することができるのだろうか。
天体の速度を測定する方法のひとつは、ドップラー効果を利用するものである。運動している天体がある元素の線スペクトル（たとえば、水素原子のHα線）を放射しているとする。それを観測して得た振動数と地上の実験室で測定したその元素の線スペクトルの振動数とのずれは天体の速度と関係している。それはよく知られているドップラー効果である。このずれから天体の速度を知ることができる。アンドロメダ銀河の速度もこの方法で測定した。宇宙物理学では、しばしば、この振動数のずれを次の式で表す。
νo＝ν（１＋ｚ）
ここで、νo は地上の実験室での振動数、νは観測された振動数である。ｚは速度が光速比べて十分小さいときにはz=v/cでありvはこの天体の速度である（この線スペクトルのずれは宇宙膨張によっても生じる。その場合、zは線スペクトルを放出した天体が存在している時期の宇宙のスケールファクターと現在の宇宙のスケールファクターの比を表している）。この方法でわかる速度は、天体の運動の我々の方向の速度成分であることに注意しよう。
4.6 宇宙の膨張則の発見
さて話をもとにもどそう。ハッブルは、アンドロメダ銀河に引き続いて、他の渦巻き星雲についてもセファイド型変光星を探し、距離の測定を試みた。同時に銀河の運動についても線スペクトルのドップラー効果を利用して測定した。その結果、我々の銀河に近づくように運動しているアンドロメダ銀河はむしろ例外で、多くの銀河は我々から遠ざかる方向に運動していることがわかった。ハッブルは1929年にこのようにして求めた銀河の距離と銀河の速度（視線方向成分）を比較したところ、ほぼ比例関係にあることを見いだした。これは非常に驚くべき発見である。さきに、一般相対論を用いた宇宙の解について述べた。フリードマンの解によると宇宙は一様に膨張している。このとき、膨張速度と距離は比例する。まさにそれに対応する観測結果をハッブルは見出したのである。この結果を発表した彼の論文の図を見ると観測データの散らばりにもかかわらず比例関係を示す線を引いたハッブルの勇気に感じ入ってしまう（佐藤文隆京大教授が有名な天文学者オールトにきいたところでは、当時の学会ではルメートルなどによって、一般相対論的な宇宙モデルでは宇宙が一様膨張することが紹介されており、このことが多くの研究者の関心を集めていたそうである。ハッブルの発見にはすでにヒントが与えられていたらしい）。ところが、この比例関係から得られる宇宙の膨張則には大きな問題があった。膨張則は、
V=H d
の関係がある。これをハッブル則と呼ぶ場合がある。ここで、Vは銀河の後退速度（ほとんどの銀河は我々から遠ざかる速度を持つのでこう呼ばれる）、dは銀河までの距離、そしてHはハッブル係数と呼ばれる宇宙の膨張を特徴づける係数である。この式とフリードマン方程式と比較するとH=(da(t)/dt)/a(t)の関係がある。この膨張がいつ始まったのかはt=d/Vで推定できる（これは、速度が一定で膨張してきた場合正しい。一般にはそうではないが）。t=d/Vにハッブル則を適用すると結局、t=1/Hとなる。これをハッブル時間と呼んでいる。ハッブル時間は宇宙の年齢の目安を与える。ハッブルがはじめて決めたHの値は、およそ530km/s/Mpcであった（Mpcは１００万パーセックを表している）。これを用いると、ハッブル時間は約２０億光年となる。これは当時知られていた地質学的に決めた地球の年齢をはるかに下回るものであった。これは何かがおかしい。宇宙膨張そのものを疑問視する人々もいた。
4.7 2種類あったセファイド変光星
この食い違いはバーデ（１９５２）がセファイドの詳細な観測をやり直すことで解決を見た。実はセファイドには２種類あって、変光の周期が同じでも、星の組成に重元素が多いセファイド（II型）は明るく、重元素が少ないセファイド（I型）は暗いのである。そして、それぞれの型のセファイド型変光星について光度周期関係が成り立っていることをバーデは示した。マゼラン星雲で観測されていたのはI型である。我々の銀河の中では、銀河面から離れたところにあるセファイドはI型で銀河面内にはII型のセファイドが分布している。銀河面内には星間ダストが分布していて恒星の光を減少させる。その結果、二つの型のセファイドを混同しても同じ光度周期関係が得られたのである。そのためシャープレイやハッブルはセファイドに二つの型があることに気がつかなかった。銀河で観測されていたセファイドはII型のセファイドで光度を実際よりも小さく見積もっていた。そのため、実際よりも銀河までの距離を小さく見積もり結果として大きなHを得てしまった。
このように、Hは宇宙の年齢と関連する重要な宇宙論的パラメータであるので、現在でも測定されつづけている。たとえば、最近もハッブル望遠鏡のキープロジェクトとして多大の観測時間をかけて測定が行われた。その方法は、８０年前にハッブルが使用した方法と同じである。つまり、銀河の中のセファイド型変光星を観測し、その変光周期と見かけの明るさを観測して最終的に距離を測定するのである。しかし、ハッブル望遠鏡が観測した領域は、ハッブルが観測したよりも、ずっと遠くのおとめ座銀河団と呼ばれる銀河の集団に属する銀河である。我々の銀河に近いと言っても、２０Mpc程度の距離にある。ハッブルキープロジェクトが最終的にきめたHは７０ｋｍ/ｓ/Mｐｃである。これによってハッブル時間は１４０億年となり、地球の年齢との食い違いはなくなっている。
ハッブル則は宇宙が膨張していることを示しているだけでなく、宇宙の年齢が有限であり、宇宙に始まりがあったことを示している。これは、当時の多くの科学者にとって受け入れがたいものであった。当時の宇宙に対する認識は宇宙は静的で、始まりも終わりもなく存在しつづけるものであったからである。ちょうど、相対論成立以前、時間が物体の運動や重力と無関係に経過するものであると常識的に考えていたように。時間に関する理解は相対論の成立によって深まった。この相対論を作ったアインシュタインが宇宙に対する見方を根本的に変更する一般相対論的宇宙論の創造にも深くかかわったのは驚くべきことであると言えよう。
ハッブル則が成り立っていると、ｚを測定することで、その銀河までの距離を推定することができる。銀河のｚは１００億光年という非常に遠い距離まで測定されている。最近ではｚ＝６近くの天体の後退速度が観測されている。人類の宇宙に対する広がりに関する認識はこの100年で太陽系の大きさから１００億光年まで約１０兆倍に広がったのである。
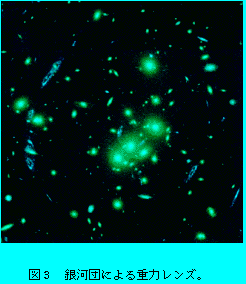
宇宙が膨張しているのなら、未来はどうなるかが疑問になるだろう。それは、宇宙のモデルを決めるもう一つの重要な物理量、宇宙の平均密度を測定する必要がある。これは、実はかなりむずかしい。問題を複雑にしているのは、光を出さない物質いわゆるダークマターが宇宙の物質のかなりの部分を占めている証拠があるからである。ダークマターが存在している証拠は多く見いだされている。その例として図３に銀河団による重力レンズの観測例を示した。重力レンズが起こるためには、光で見えない質量が大量に存在することが示されている。しかし、その正体については未知の素粒子などの可能性が指摘されているが不明である。
現在の宇宙が膨張しているとすると、時間をさかのぼると宇宙はどんどん収縮することになる。このため密度は増大する。この時、宇宙の物質はどうなっていたのか。これについては次回述べることにしよう。次回は、宇宙膨張は物質の生成や元素の起源について解説しよう。これらに対する理解も２０世紀に大きく進んだのである。
５ すばる望遠鏡
最後に、最近の話題を取り上げておこう。第一回目、はすばる望遠鏡についてである。２１世紀を前にして、日本の天文学に強力な大型観測装置が誕生した。1999年にFIRST LIGHTを迎えたすばる望遠鏡である。このすばる望遠鏡は口径８ｍの一枚鏡をもつ世界最大級の望遠鏡である。すばる望遠鏡は大気の影響をできるだけ避けるためハワイのマウナケア島の山頂に建設された。マウナケア山頂は約４０００ｍの高度にあり、アメリカのKEK望遠鏡（口径１０ｍ）をはじめ世界の巨大な望遠鏡が集中している観測適地である。すばる望遠鏡の特徴は、その口径の大きさとともに、主光学系の性能が高いことである。その性能の高さは、0.2"（１"は１秒角と呼ばれ3600分の一度のことである）の空間分解能をすばるファーストライトで達成したことでも示されている。この成功の理由には、従来球形のドームを円筒形にすることでドーム内の気流の乱れを極力抑えたこと、active supportの主鏡を用いることで口径8.2mにもかかわらず厚みをわずか20cmとし、２６１のアクチュエータで鏡の歪みを補正することに成功していることなどがあげられる。後者はたとえて言えば、やわやわのゼリーのような鏡を多数の支持棒でコントロールして支えることでゆがみの小さな鏡を実現した技術の成果である。すばる望遠鏡は、大きな口径と高い分解能によって遠方の銀河の観測などの観測を進め宇宙論と銀河進化に関して興味ある成果をあげることが期待されている。また、高い空間分解能を生かして、星形成や惑星系形成でも重要な成果をあげると期待されている。現在、高いスペクトル分解能を持った観測装置などをすばる望遠鏡に装着する作業が続けられている。その中には、明るい天体のそばの暗い天体を見るための特殊な装置や、大気の揺らぎを特殊な光学系を用いることで補正することができる補償光学装置などがあり本格的な観測が期待される。最近の情報は、すばる望遠鏡のインターネットホームページはhttp://www.nao.ac.jp/Subaru/で知ることができる。
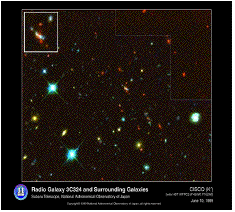
図４ すばる望遠鏡による１００億年かなたの銀河（写真のほぼ中央）の観測。左上の四角の中の銀河が１００億光年のかなたの銀河の拡大図である。